 雑記
雑記 数学の勉強法 大学入試編
大学入試対策としての数学の勉強法をレクチャーしようと思います。とはいっても高校の定期テストから共通テスト、私立大学や国公...
 雑記
雑記  雑記
雑記  入試問題解説
入試問題解説 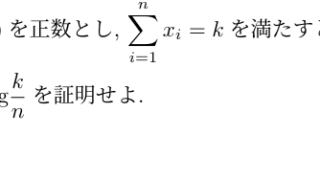 入試問題解説
入試問題解説  大学数学
大学数学  問題解説
問題解説  整数
整数