今回は極限の計算問題について解説しようと思います。全何回になるかわかりませんが、受験において非常に大切な分野ですから、深く解説したいと思います。
それでは、まず1問目はこちらです。
次の極限を求めよ.
$\displaystyle\lim_{n\to\infty}\Bigg(\ \dfrac{1}{\sqrt{n}}+\dfrac{2}{\sqrt{n}}+\cdots+\dfrac{n}{\sqrt{n}}\Bigg)$
「自然数の逆数の和の極限が$\infty$になることを知っていれば本問も$\infty$になると予想できます。(この事実は証明も含めて知っておきましょう。)」
よって$\infty$ にもっていくには追い出しの原理を用いようと考えます。この場合, 最小の項は$\dfrac{1}{\sqrt{n}}$なので, すべての項を$\dfrac{1}{\sqrt{n}}$に置き換えて不等式を作ります.。そうすることで$\infty$にもっていけるわけです。
では解答です。
$S_n=\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\cdots+\dfrac{1}{\sqrt{n}}$とおく.
$1\leqq k\leqq n$である$k$に対して,
$\dfrac{1}{\sqrt{k}}\geqq\dfrac{1}{\sqrt{n}}$
であるから,
$S_n\geqq\dfrac{1}{\sqrt{n}}+\dfrac{1}{\sqrt{n}}+\cdots+\dfrac{1}{\sqrt{n}}$
=$n\cdot\dfrac{1}{\sqrt{n}}$
=$\sqrt{n}\rightarrow\infty$
である.
よって, $\displaystyle\lim_{n\to\infty}S_n=\infty\cdots\cdots$(答)
続いてはこちらです。
$\displaystyle\lim_{x\to\pi}\dfrac{\sqrt{a+\cos x}-b}{(x-\pi)^2}=\dfrac{1}{4}$
では、解答です。
分母について、$\displaystyle\lim_{t\to 0}t^2=0$であるから、題意を満たすためには分子について$\displaystyle\lim_{t\to 0}(\sqrt{a-\cos t}-b)=0$であることが必要である。
これを解くと、$b=\sqrt{a-1}$であるので、与式に代入すると
$\displaystyle\lim_{t\to 0}\dfrac{\sqrt{a-\cos t}-\sqrt{a-1}}{t^2}$=$\displaystyle\lim_{t\to 0}\dfrac{1-\cos t}{t^2} \cdot \dfrac{1}{\sqrt{a-\cos t}+\sqrt{a-1}}$=$\dfrac{1}{2} \cdot \dfrac{1}{2\sqrt{a-1}}$
となる。
これが$\dfrac{1}{4}$である条件は$a=2, b=1$である。$\cdots \cdots$(答)
では、解答です。
$-1\leqq\cos n\leqq 1$であるから、
$-\dfrac{1}{n}\leqq\dfrac{1}{n} \cos n\leqq \dfrac{1}{n}$が成立する。
$n\to\infty$のとき、$\dfrac{1}{n}\to 0$であるから、はさみうちの原理より
与式 = $0 \cdots\cdots$(答)
である。
ガウス記号は実数$x$に対して$x$以下で最大の整数を表す記号であり、$\left[x\right]$と表す。
・$\left[x\right]$は整数である
・$\left[x\right]\leqq x < \left[x\right]+1$ ・$x-1 < \left[x\right]\leqq x$ が成立する。 たとえば、$\left[\dfrac{7}{2}\right]=3, \left[-1.5\right]=-2$である。
実数$a$に対して$n\leqq a < n+1$を満たす整数$n$を記号$\left[a\right]$で表す。次の問いに答えよ。 (1) $\left[-3.1\right]$を求めよ。 (2) $\left[\sqrt{800}\right]=10x$となる$x$を求めよ。 (3) $\left[19x-1\right]=10x$となる$x$を求めよ。 (4) $\left[x^2+6x-4\right]=10x$となるすべての$x$を求めよ。
ガウス記号の定義に戻って確認するだけです。
(1) $$-4\leqq -3.1 < -3$$ より求める値は$$-4\cdots\cdots(答)$$ (2) $$28^2<800<29^2$$ より$$28<\sqrt{800}<29$$ であるので、 $$\left[\sqrt{800}\right]=28ゆえ、x=\dfrac{14}{5}\cdots\cdots(答)$$ (3)ガウス記号の定義より、 $$10x\leqq 19x-1<10x+1$$ $$\therefore \dfrac{1}{9}\leqq x<\dfrac{2}{9}$$ が成立するので、 $$\dfrac{10}{9}\leqq 10x<\dfrac{20}{9}$$ である。 $10x$は整数であるので、$$10x=2より、x=\dfrac{1}{5}\cdots\cdots(答)$$ (4) 同様に考えると、 $$10x\leqq x^2+6x-4<10x+1$$であるので、$$-1< x \leqq 2-2\sqrt{2}$$ $$ 2+2\sqrt{2} \leqq x < 5$$ が成立。 したがって、$$-10 < 10x \leqq 20-20\sqrt{2}$$ $$20+20\sqrt{2} \leqq 10x < 50$$ となり、$10x$は整数であるので$$10x = -9, 49$$ $$\therefore x = -\dfrac{9}{10}, \dfrac{49}{10}\cdots\cdots(答)$$
極限でガウスが出てきたら基本ははさみうちの原理を用います。上の公式を見てもわかる通り不等式で定義されているのでイメージはしやすいと思います。不等式を使ってガウス記号$\left[\right]$を外します。
$$\dfrac{2}{n}(\dfrac{n}{5}-1) < \dfrac{2}{n}\left[\dfrac{n}{5}\right]\leqq\dfrac{2}{n}\cdot\dfrac{n}{5}$$ である。 ここで、 $$\displaystyle\lim_{n\to\infty}\dfrac{2}{n}(\dfrac{n}{5}-1)=\displaystyle\lim_{n\to\infty}(\dfrac{2}{5}-\dfrac{2}{n})$$ $$=\dfrac{2}{5}$$ と $$\displaystyle\lim_{n\to\infty}\dfrac{2}{n}\cdot\dfrac{n}{5}=\displaystyle\lim_{n\to\infty}\dfrac{2}{5}$$ $$=\dfrac{2}{5}$$ を合わせて、はさみうちの原理より $$\displaystyle\lim_{n\to\infty}\dfrac{2}{n}\left[\dfrac{n}{5} \right]=\dfrac{2}{5}$$ である。
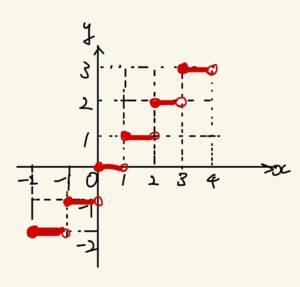
上図のようになるので、
$$\displaystyle\lim_{x\to 2+0}\left[x\right]=2$$
$$\displaystyle\lim_{x\to 2-0}\left[x\right]=1$$
となり、$\displaystyle\lim_{x\to 2}\left[x\right]$は存在しない。したがって、関数$\left[x\right]$は$x=2$において不連続である。
極限の概算というものについて解説したいと思います。
たとえば、$n\to\infty$のとき$n$を100000000(1億)とでもイメージすると、$n+1$は100000001(1億1)となり1億と大して変わりませんよね。こういうとき、この1みたいなものを「カス」や「ゴミ」と言ったりします。そのようなものなので切り捨ててもよいわけです。したがって、この場合は1億とします。このように$n$がめちゃくちゃ大きいときそれに付いている定数は捨ててしまうと見やすくなるので、そういうイメージをもつことは非常に大切です。
(1) $\displaystyle\lim_{n\to\infty}\dfrac{\log (3n+2)}{\log (2n^2+3)}$
(2) $\displaystyle\lim_{x\to\infty}(\cos^2\sqrt{x+1}+\sin^2\sqrt{x})$
では続いて分母はどうなるか考えてみましょう。$\log (2n^2+3)\fallingdotseq \log (2n^2)\fallingdotseq \log n^2 + \log 2\fallingdotseq 2\log n$となるので、分子とあわせて、$\dfrac{\log n}{2\log n}=\dfrac{1}{2}$となります。ただし、これを答案に書くのはダメです。なぜなら、$\fallingdotseq$というのは数学において定義されていないからです。あくまでもイメージというだけなので、論理性がないため不適です。イメージといっても間違えることはありません。必ずこういう風に考えていけば正解です。検算や答えのみを書くタイプの試験では有効です。
では、解答です。
$$=\displaystyle\lim_{n\to\infty}\dfrac{\log n+\log(3+\dfrac{2}{n})}{\log n^2+\log(2+\dfrac{3}{n^2})}$$$$=\displaystyle\lim_{n\to\infty}\dfrac{1+\log(3+\dfrac{2}{n})\cdot\dfrac{1}{\log n}}{2+\log(2+\dfrac{3}{n^2})\cdot\dfrac{1}{\log n}}$$$$=\dfrac{1+\log3\cdot 0}{2+\log2 \cdot 0}$$
$$=\dfrac{1}{2}\cdots\cdots(答)$$
いま、$x\to\infty$であるので$\sqrt{x+1}\fallingdotseq\sqrt{x}$です。
したがって、$\cos^2\sqrt{x+1}+\sin^2\sqrt{x}\fallingdotseq\cos^2\sqrt{x}+\sin^2\sqrt{x}=1$とみなすことができ答えだけなら一瞬でわかります。
答えが先にわかっているので、逆算的に考えます。$\cos^2\sqrt{x}+\sin^2\sqrt{x}$の形を無理やり作ります。($\cos^2\sqrt{x+1}\fallingdotseq\cos^2\sqrt{x}$となることが分かっているからです。)
そうすると今度はつじつま合わせで残った、$\cos^2\sqrt{x+1}-\cos^2\sqrt{x}$が0になることを言わないといけません。まず倍角公式を用いて2乗をなくしましょう。その後、$x\to\infty$の世界でどうなるか考えればいいですが、必ず答えは0になります。
では、しっかりと答案を作っていきましょう。
$$f(x)=(\cos^2\sqrt{x}+\sin^2\sqrt{x})+(\cos^2\sqrt{x+1}-\cos^2\sqrt{x})$$
$$=1+(\cos^2\sqrt{x+1}-\cos^2\sqrt{x})\cdots\cdots①$$
と表せる。
ここで、$$\cos^2\sqrt{x+1}-\cos^2\sqrt{x}$$
$$=\dfrac{1+\cos 2\sqrt{x+1}}{2}-\dfrac{1+\cos 2\sqrt{x}}{2}$$
$$=\dfrac{1}{2}(\cos 2\sqrt{x+1}-\cos 2\sqrt{x})$$
$$=-\sin(\sqrt{x+1}+\sqrt{x})\sin(\sqrt{x+1}-\sqrt{x})$$
$$=-\sin(\sqrt{x+1}+\sqrt{x})\sin\dfrac{1}{\sqrt{x+1}+\sqrt{x}}$$
のように変形でき、$$|\sin(\sqrt{x+1}+\sqrt{x})|\leqq 1$$
$$\displaystyle\lim_{x\to\infty}\sin\dfrac{1}{\sqrt{x+1}+\sqrt{x}}=0$$
であるので、
$$\displaystyle\lim_{x\to\infty}(\cos^2\sqrt{x+1}-\cos^2\sqrt{x})=0$$
である。
したがって、①から、$$\displaystyle\lim_{x\to\infty}f(x)=1\cdots\cdots(答)$$



コメント