$\alpha, \beta, \gamma$は
$$\alpha > 0, \beta > 0, \gamma > 0, \alpha+\beta+\gamma=\pi$$
を満たすものとする。このとき、$\sin\alpha\sin\beta\sin\gamma$の最大値を求めよ。
$$\alpha > 0, \beta > 0, \gamma > 0, \alpha+\beta+\gamma=\pi$$
を満たすものとする。このとき、$\sin\alpha\sin\beta\sin\gamma$の最大値を求めよ。
出典 : 京都大
$\alpha, \beta, \gamma$の変域から、それぞれ三角形の内角になっていることに気づきたいところです。$\sin$絡みの問題なので正弦定理を用います。
半径1の円に内接している三角形$ABC$を考えて、正弦定理から
$$\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}=2$$
です。よって、
$$\sin\beta=\dfrac{b}{2}, \sin\gamma=\dfrac{c}{2}$$
なので、
$$\sin\alpha\sin\beta\sin\gamma=\dfrac{1}{2}\cdot\dfrac{1}{2}bc\sin\alpha$$
となります。
したがって、三角形$ABC$の面積$\dfrac{1}{2}bc\sin\alpha$の最大値を求める問題に帰着されます。
問題文だけでは「三角形」という言葉は出てきませんが、与えられた$\alpha, \beta, \gamma$の条件を考えると「三角形の内角だ!」と気づけます。そうすると正弦定理を用いる発想も出てきます。
では、解答です。
半径1の円に内接している三角形$ABC$を考えて、正弦定理から
$$\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}=2$$
です。よって、
$$\sin\beta=\dfrac{b}{2}, \sin\gamma=\dfrac{c}{2}$$
なので、
$$\sin\alpha\sin\beta\sin\gamma=\dfrac{1}{2}\cdot\dfrac{1}{2}bc\sin\alpha$$
となります。
したがって、三角形$ABC$の面積$\dfrac{1}{2}bc\sin\alpha$の最大値を求める問題に帰着されます。
問題文だけでは「三角形」という言葉は出てきませんが、与えられた$\alpha, \beta, \gamma$の条件を考えると「三角形の内角だ!」と気づけます。そうすると正弦定理を用いる発想も出てきます。
では、解答です。
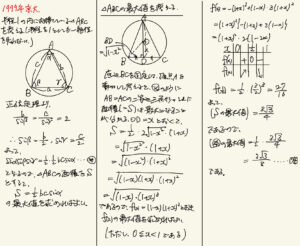
解答内で$S=\sqrt{〇〇}$の式がありましたが、すべてルートの中に入れてしまいましょう。そうすると微分するときにルートが関係なくなるので微分しやすいです。この手法はよく使うので覚えておきましょう。



コメント