今回は1990年の東工大の問題を解説します。
この問題はいわゆる凸不等式といわれるもので、解き方は決まっています。グラフの凸性を考慮して、不等式を作っていきます。
解答(1990 東工大)
$y=x\log x$について、
$$y'=\log x+1, y''=\dfrac{1}{x}$$
となるので、$x > 0$において、$y'' > 0$ゆえ、$y=x\log x$のグラフは下に凸である。・・・・・①
ここで、グラフ上の点を$(t, t\log t)$とおくと、その点における接線の方程式は
$$y=(\log t+1)x-t$$
であるので、①と合わせて、
$$x\log x\geqq (\log t+1)x-t・・・・・②$$
が成り立つ。いま、$t, n, k$は正なので、$t=\dfrac{k}{n}$としてもよく、②に$x=x_1, x_2, \cdots, x_n$を代入し、それらの和を辺々からとると、
$$\displaystyle\sum_{i=1}^n x_i\log x_i\geqq\displaystyle\sum_{i=1}^n\{(\log\dfrac{k}{n}+1)x_i-\dfrac{k}{n}\}$$
$$y'=\log x+1, y''=\dfrac{1}{x}$$
となるので、$x > 0$において、$y'' > 0$ゆえ、$y=x\log x$のグラフは下に凸である。・・・・・①
ここで、グラフ上の点を$(t, t\log t)$とおくと、その点における接線の方程式は
$$y=(\log t+1)x-t$$
であるので、①と合わせて、
$$x\log x\geqq (\log t+1)x-t・・・・・②$$
が成り立つ。いま、$t, n, k$は正なので、$t=\dfrac{k}{n}$としてもよく、②に$x=x_1, x_2, \cdots, x_n$を代入し、それらの和を辺々からとると、
$$\displaystyle\sum_{i=1}^n x_i\log x_i\geqq\displaystyle\sum_{i=1}^n\{(\log\dfrac{k}{n}+1)x_i-\dfrac{k}{n}\}$$
である。
いま、$\displaystyle\sum_{i=1}^n x_i=k$であるから、
$$\displaystyle\sum_{i=1}^n x_i\log x_i\geqq k(\log\dfrac{k}{n}+1)-n\cdot\dfrac{k}{n}=k\log\dfrac{k}{n}$$
であるので示された。
別解(1990 東工大)
$y=\log x$の$(1, 0)$における接線が
$$y=x-1$$
であるから、$y=\log x$が上に凸であることとあわせて、
$$\log x\leqq x-1$$
が成り立つ。したがって、
$$k\log\dfrac{k}{n}-\displaystyle\sum_{i=1}^n x_i\log x_i$$
$$=\log\dfrac{k}{n}\displaystyle\sum_{i=1}^n x_i-\displaystyle\sum_{i=1}^n x_i\log x_i$$
$$y=x-1$$
であるから、$y=\log x$が上に凸であることとあわせて、
$$\log x\leqq x-1$$
が成り立つ。したがって、
$$k\log\dfrac{k}{n}-\displaystyle\sum_{i=1}^n x_i\log x_i$$
$$=\log\dfrac{k}{n}\displaystyle\sum_{i=1}^n x_i-\displaystyle\sum_{i=1}^n x_i\log x_i$$
$$=\displaystyle\sum_{i=1}^n x_i (\log\dfrac{k}{n}-\log x_i)$$
$$=\displaystyle\sum_{i=1}^n x_i\log\dfrac{k}{nx_i}$$
$$\leqq\displaystyle\sum_{i=1}^n x_i(\dfrac{k}{nx_i}-1)$$
$$=\displaystyle\sum_{i=1}^n (\dfrac{k}{n}-x_i)$$
$$=n\cdot\dfrac{k}{n}-\displaystyle\sum_{i=1}^n x_i$$
$$=0$$
$\therefore \displaystyle\sum_{i=1}^n x_i\log x_i\geqq k\log\dfrac{k}{n}$である。

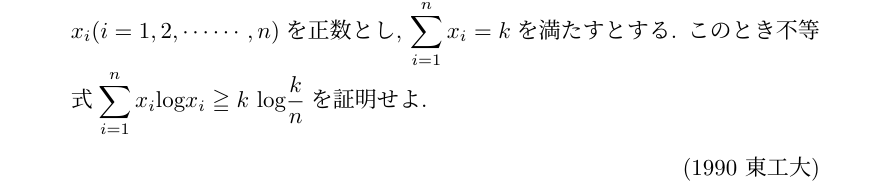


コメント